对于多约束条件的多目标优化问题，像遗传算法或者进化算法有比较好的算法推荐吗？

最近遇到一个电路参数的优化问题，里面会有很多的约束条件，同时其不具备有线性关系，像各种遗传算法五花八门，该怎么选择呢

答主找到了么！我也遇见了

多目标法

在多目标模型中，将约束视为一个附加目标或多个附加目标，将CMOP转化为无约束的对应对象，然后利用moea求解转换后的问题。

近年算法整理

1、约束被转化为两个新的目标:一个是基于惩罚函数的目标，另一个是等于违反约束个数的目标。
2、Ray等在约束违反测度的基础上增加了新的目标，设计了一种不可行的驱动进化算法，促使种群从不可行的区域向约束边界靠近。
3、Isaacs等将约束作为新的目标，将原有m个目标的约束最小化问题重新定义为m + 1个目标的无约束最小化问题。
4、Long构造了一种求解cmp问题的新CHT，将得到的解的收敛性、多样性和可行性作为多目标子问题的三个新目标。
5、Peng等以约束违反程度为新目标，设计了一种新的基于有向权的CHT求解cops，利用分布在可行区域和不可行区域的两种权分别引导搜索到有希望区域。
6、Zhou等提出了一个三目标进化框架来解决约束多目标问题。该框架将约束条件转化为可行性指标，再与收敛性指标和多样性指标相结合，形成三个新的目标。

基于自适应启动策略的混合交叉动态多目标优化算法（Mixture Crossover Dynamic Constrained Multi-objective Evolutionary Algorithm Based on Self-Adaptive Start-Up Strategy, MC-DCMOEA）由耿焕同等人于2015年提出，其基于自适应冷热启动、混合交叉算子与精英群体的局部搜索等技术方法，力求克服单独采用冷启动方式而出现再次收敛速度慢、单种交叉算子 自适应不够以及正态变异多样性程度偏弱等问题。MC-DCMOEA算法描述如下：

参考文献：

[1]GENG Huan-Tong,SUN Jia-Qing,JIA Ting-Ting. A Mixture Crossover Dynamic Constrained Multi-objective Evolutionary Algorithm Based on Self-Adaptive Start-Up Strategy[J]. Pattern Recognition and Artificial Intelligence, 2015, 28(5): 411-421.

现实生活中,存在许多动态多目标优化问题(Dynamic Multi-objective Optimization Problems,DMOPs),这类问题的目标函数之间相互矛盾,并且目标函数、约束或者参数都可能随着时间的变化而发生变化.这种随时间不断变化的特性,给解决DMOPs带来了挑战,算法不仅要能够追踪到最优解,同时还要求算法能够快速地对发生的变化做出响应。其中，动态约束多目标优化（Dynamic Constrained Multiobjective Optimization，DCMO）是动态多目标优化问题中的一种，其问题较为复杂且求解难度大。动态约束多目标优化（Dynamic Constrained Multiobjective Optimization，DCMO）测试函数DCF1~DCF10的turePF_IT猿手的博客-CSDN博客

Benchmark Problems for CEC2023 Competition on Dynamic Constrained Multiobjective Optimization中共包含10测试函数，其详细信息如下：

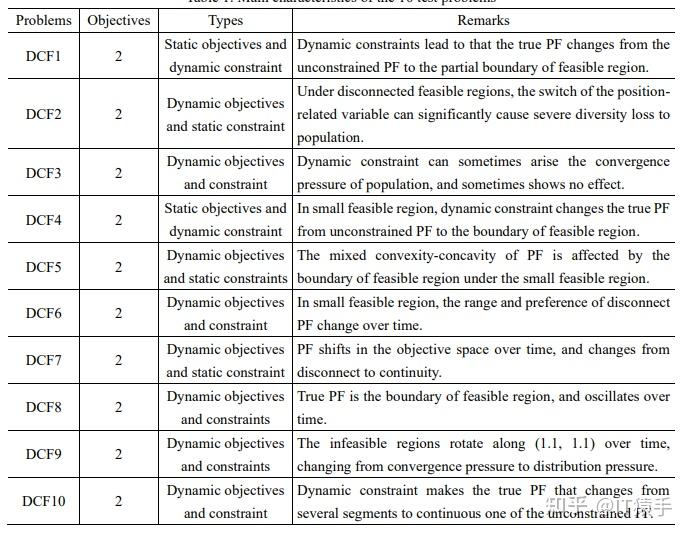
每个测试函数的环境变化程度、环境变化频率和最大迭代次数考虑如下八种情形：

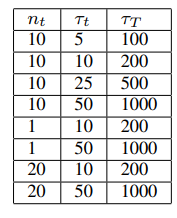
设置种群大小为100，外部存档大小为200，以DCF5为例，当取第1组参数设置时，即环境变化程度、环境变化频率 和最大迭代次数分别为10/5/100，其代码如下：（代码中更改TestProblem以此选择不同测试函数1-10，更改group选择不同参数设置1-8，相对于共有80种情形可供选择）

close all;
clear ; 
clc;
warning off
addpath('https://www.zhihu.com/question/DCF')
addpath('https://www.zhihu.com/question/DCF-PF')
%% 基于自适应启动策略的混合交叉动态约束多目标优化算法（MCDCMOEA）
%reference code link: https://mbd.pub/o/bread/mbd-ZJuUmJ9r
TestProblem=5;%选择测试函数1-10（可以自己修改）
group=1;%选择参数1-8 （可以自己修改）
MultiObj=GetFunInfoCec2023(TestProblem);%获取测试问题维度、目标函数、上下限、目标个数等信息
paramiter=GetFunParamiter(group);%获取参数nt taut maxgen
% 参数设置
params.Np=100;        %Np 种群大小 （可以自己修改）
params.Nr=200;        %Nr 外部存档大小 （可以自己修改） 注意：外部存档大小Nr不能小于种群大小Np
params.nt=paramiter(1); % nt 环境变化程度
params.taut=paramiter(2);% taut 环境变化频率  
params.maxgen=paramiter(3);%maxgen 最大迭代次数


%% 基于自适应启动策略的混合交叉动态约束多目标优化算法（MCDCMOEA）求解，结果为Result
Result=MCDCMOEA(params,MultiObj);


%% 获取真实的POF
POF_Banchmark=getBenchmarkPOF(TestProblem,group);
for i=1:size(POF_Banchmark,2)
    Result(i).TruePOF=POF_Banchmark(i).PF;
end


%% 计算GD IGD HV Spacing
for k=1:size(Result,2)
     Result(k).GD=GD(Result(k).PF,Result(k).TruePOF);
     Result(k).IGD=IGD(Result(k).PF,Result(k).TruePOF); 
     Result(k).HV=HV(Result(k).PF,Result(k).TruePOF);
     Result(k).Spacing=Spacing(Result(k).PF);%计算性能指标SP
end
%% 保存结果
save Result Result %保存结果
PlotResult;






    

由于测试函数共有10个，且每个测试函数均有8种参数可供选择，因而共有80种选择方案。由于篇幅限制，下面仅以DCF3、DCF5和DCF7为例，采用MCDCMOEA求解。测试其余函数只需修改代码中TestProblem和group的值。

（1）DCF3

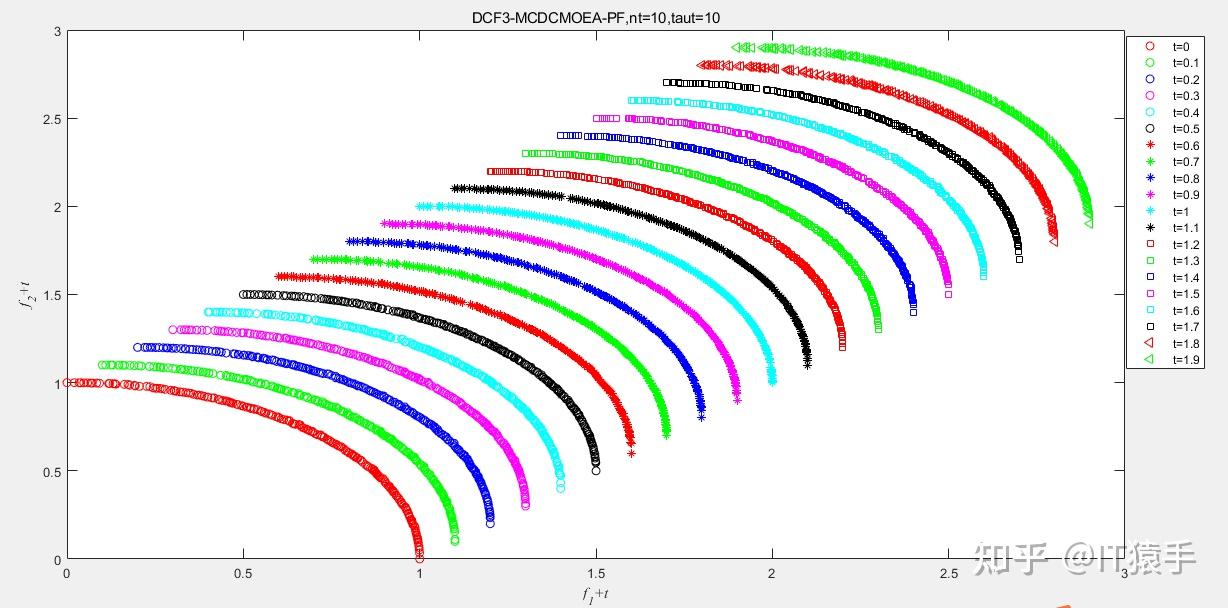
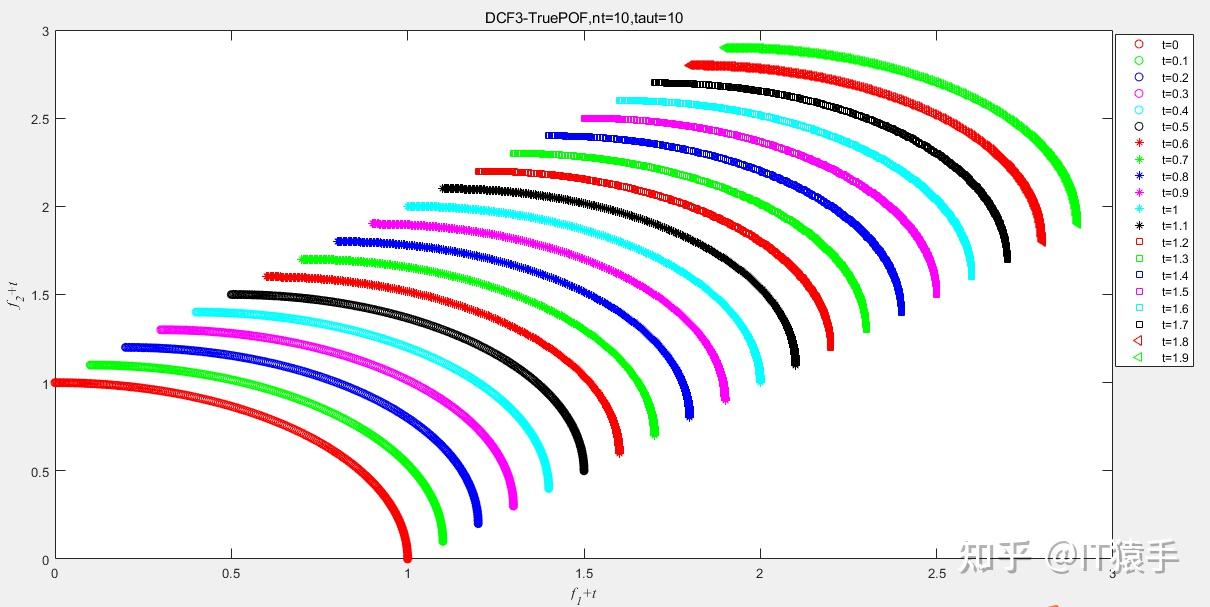
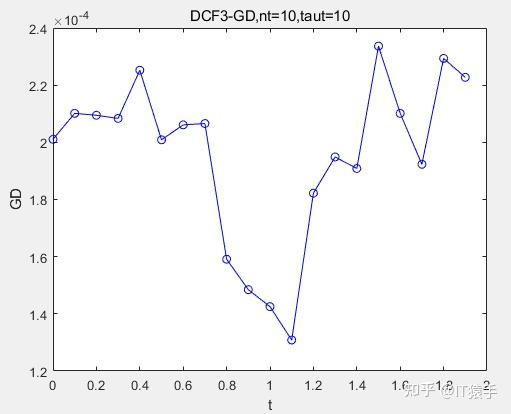
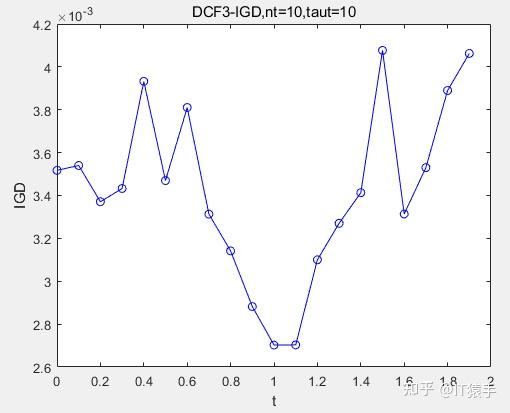
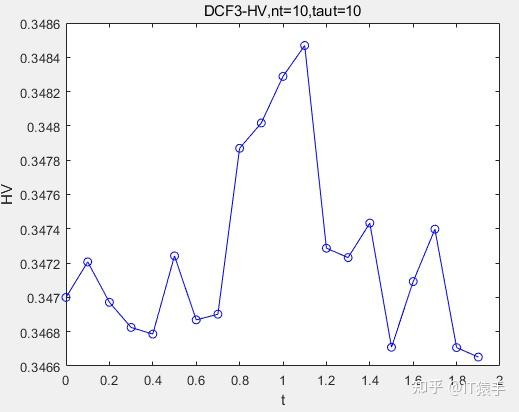
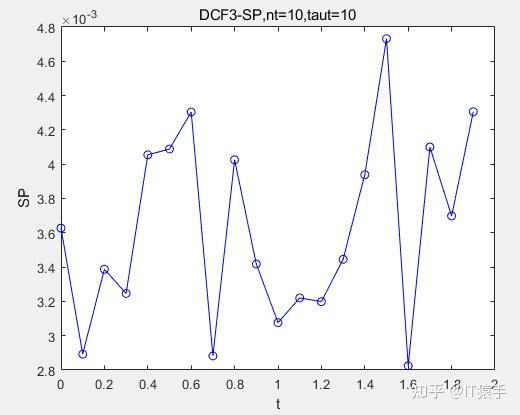
（2）DCF5

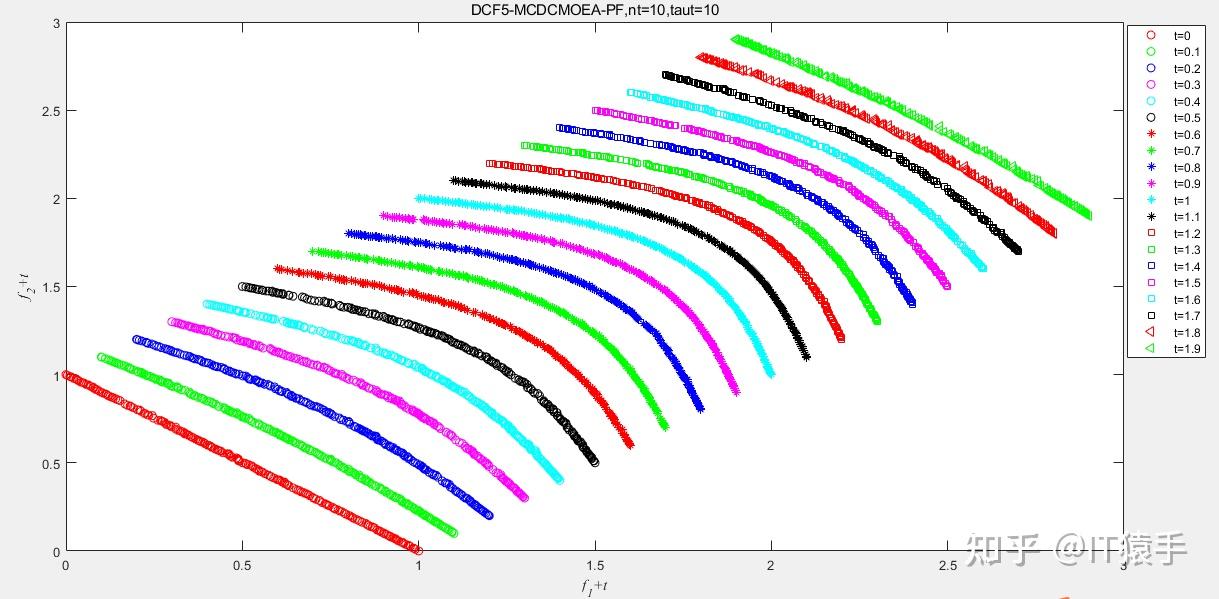
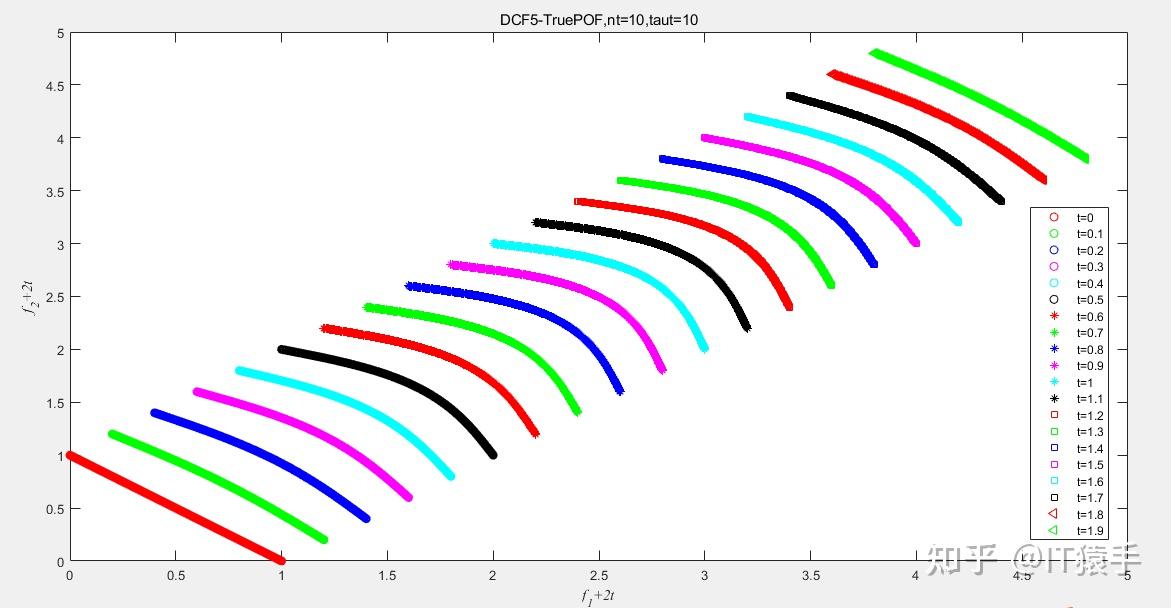
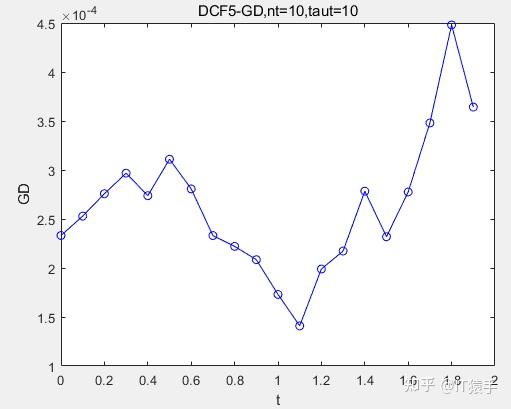
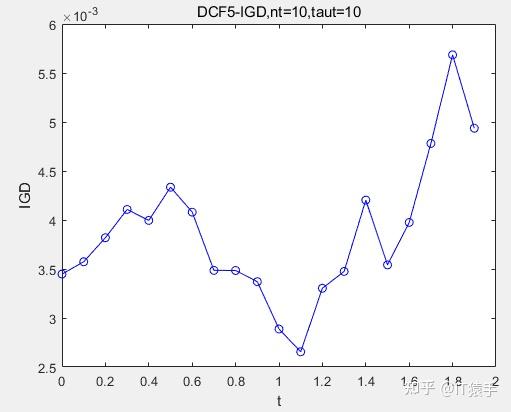
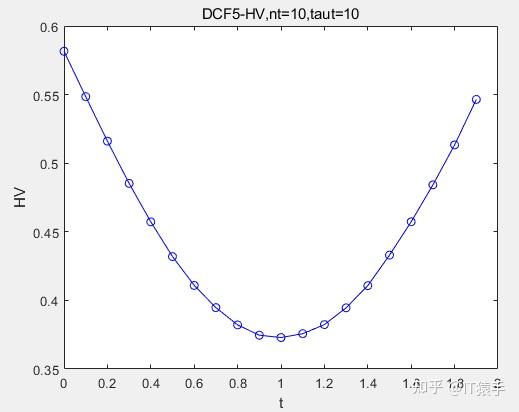
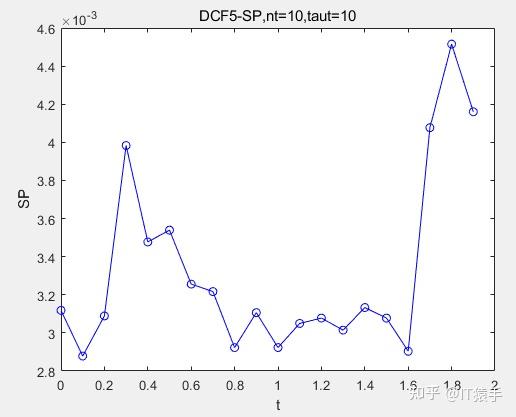
（3）DCF7

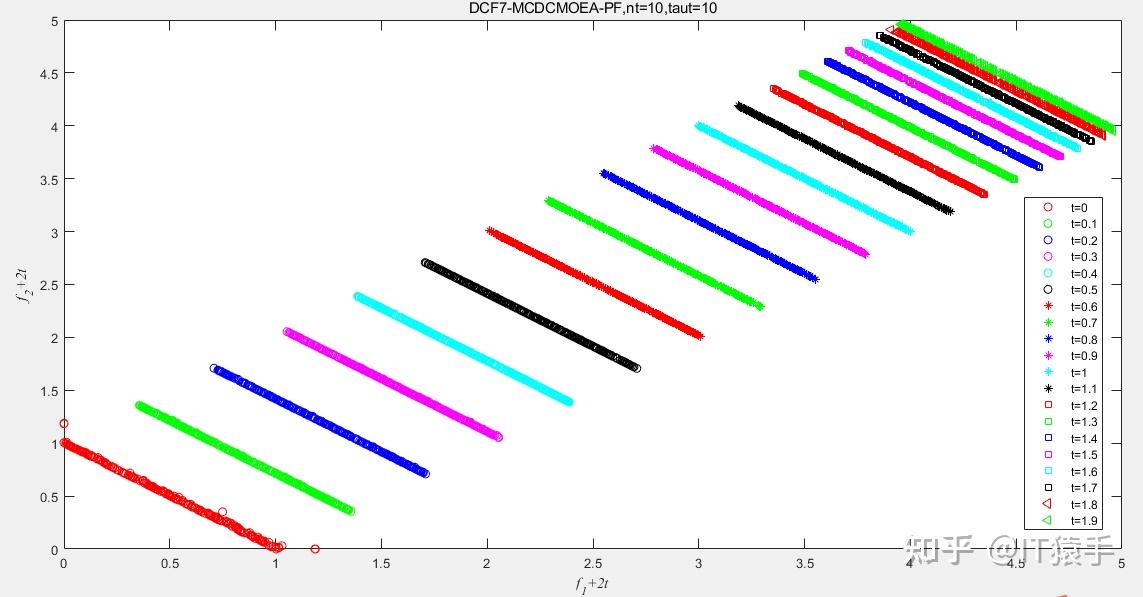
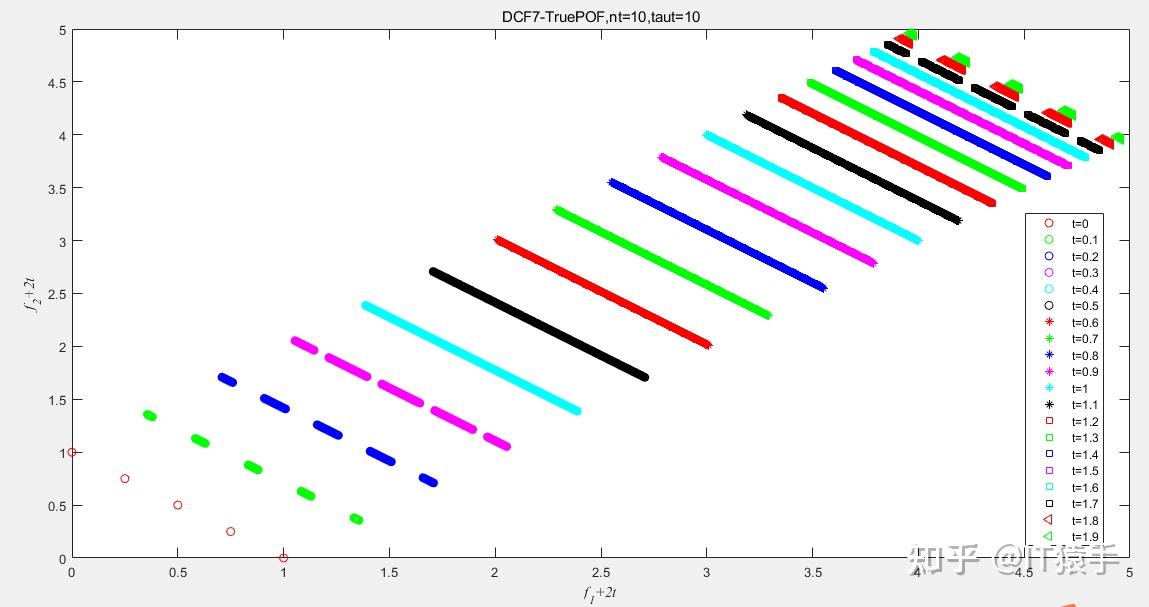
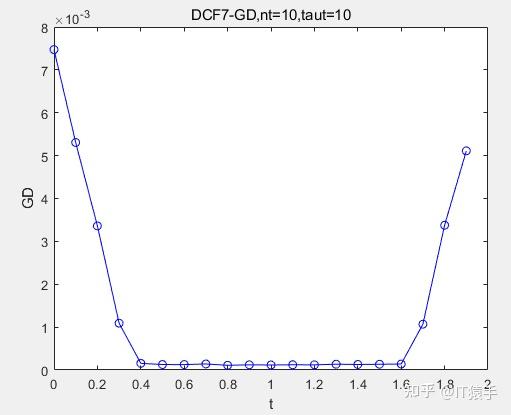
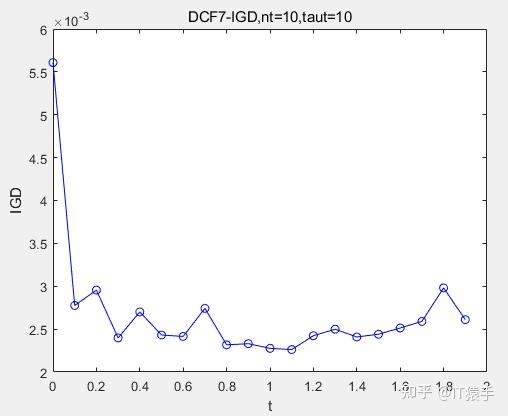
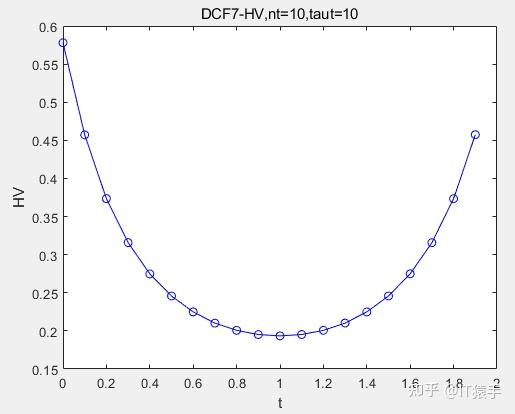
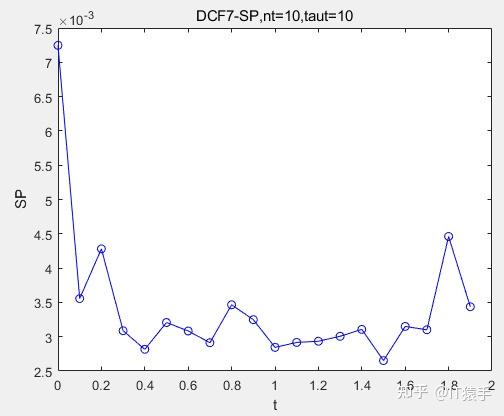
去看了《IEEE Trans. on Evolutionary Computation》、《Evolutionary Computation》、《IEEE Trans. on Cybernetics》、《IEEE Trans. on Systems Man Cybernetics-systems》、《Expert Systems with Applications》、《Knowledge-based Systems》、 《Information Sciences》、《Congress on Evolutionary Computation (CEC)》相关期刊的文章。